NumPy 快速入门教程
NumPy 快速入门教程
ytkz欢迎体验 NumPy 的强大功能!NumPy 是 Python 中用于科学计算的核心库,特别适合处理多维数组和矩阵运算。本教程将带你快速上手 NumPy,面向零基础或初学者,涵盖数组创建、操作、索引等核心概念。
先决条件
在开始之前,你需要:
- 基础 Python 知识:了解列表、元组、循环等基本概念。如需复习,可参考 Python 官方教程。
- 安装 NumPy:通过 pip install numpy 安装 NumPy。
- 安装 Matplotlib(可选):部分示例(如直方图)需要 Matplotlib,可通过 pip install matplotlib 安装。
注意:本教程假设你已安装 Python 环境并能运行代码。如果你是新手,推荐使用 Jupyter Notebook 或 VS Code 来运行代码,方便交互式学习。
学习者概况
本教程是 NumPy 数组的入门指南,重点讲解如何表示和操作 n 维数组(ndarray)。如果你:
- 不清楚如何对 n 维数组应用常见函数(无需 for 循环);
- 想了解数组的 轴(axis) 和 形状(shape) 属性;
- 希望快速掌握 NumPy 的核心功能,
那么这篇教程将非常适合你!
学习目标
通过本教程,你将能够:
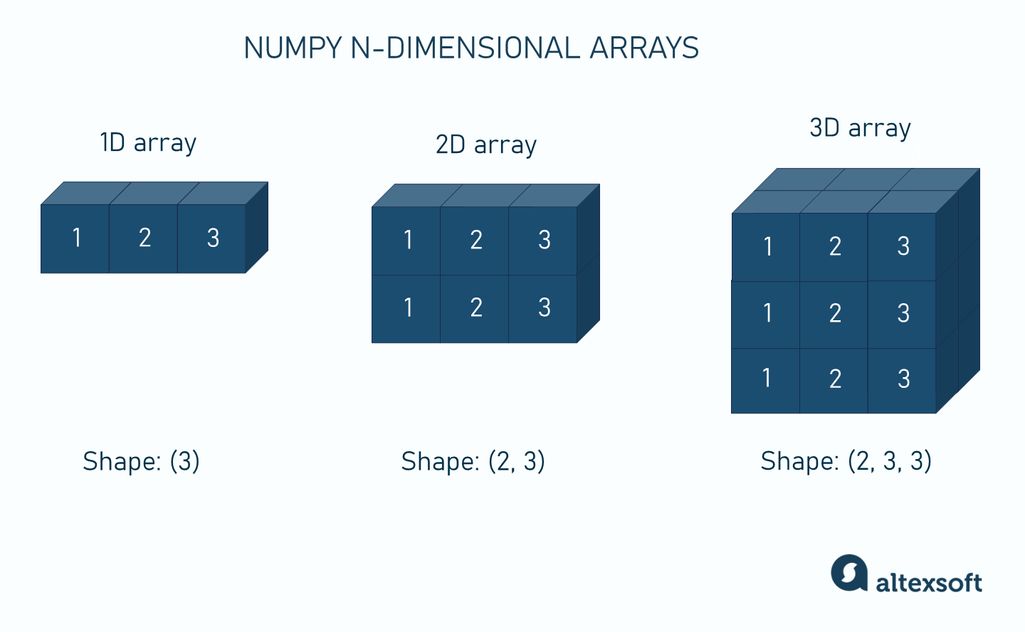
- 理解 NumPy 中一维、二维及 n 维数组的区别;
- 学会在不使用 for 循环的情况下进行线性代数运算;
- 掌握 n 维数组的 轴(axis) 和 形状(shape) 属性。
NumPy 基础
NumPy 的核心对象是 ndarray,即同构多维数组。它是一个由相同类型元素(通常是数字)组成的表格,通过非负整数元组进行索引。在 NumPy 中,维度 被称为 轴(axis)。
什么是轴(Axis)?
一维数组:只有一个轴。例如,[1, 2, 1] 表示三维空间中的一个点,轴的长度为 3。
二维数组:有两个轴。例如:
[[1., 0., 0.], [0., 1., 2.]]这里第一个轴(行)长度为 2,第二个轴(列)长度为 3。
注意:NumPy 的 numpy.array 与 Python 标准库的 array.array 不同,后者仅支持一维数组且功能有限。
ndarray 的重要属性
以下是 ndarray 的核心属性,理解它们对后续操作至关重要:
| 属性 | 描述 |
|---|---|
| ndim | 数组的轴数(维度)。例如,二维数组的 ndim 为 2。 |
| shape | 数组的维度,表示每个轴的大小。例如,(n, m) 表示 n 行 m 列。 |
| size | 数组元素的总数,等于 shape 中各维度的乘积。 |
| dtype | 元素的数据类型,例如 int32、float64 或 complex128。 |
| itemsize | 每个元素的大小(以字节为单位)。例如,float64 的 itemsize 为 8(64/8)。 |
| data | 包含数组实际元素的缓冲区(通常无需直接访问)。 |
示例:创建并检查数组
以下代码展示如何创建数组并查看其属性:
import numpy as np
# 创建一个 3x5 的二维数组
a = np.arange(15).reshape(3, 5)
print(a)
# 输出:
# [[ 0 1 2 3 4]
# [ 5 6 7 8 9]
# [10 11 12 13 14]]
print(a.shape) # (3, 5)
print(a.ndim) # 2
print(a.dtype.name) # 'int64'
print(a.itemsize) # 8
print(a.size) # 15
print(type(a)) # <class 'numpy.ndarray'>
# 创建一维数组
b = np.array([6, 7, 8])
print(b) # [6 7 8]
print(type(b)) # <class 'numpy.ndarray'>数组创建
NumPy 提供了多种创建数组的方法。以下是常见的几种方式:
1. 从 Python 列表或元组创建
使用 np.array() 将 Python 列表或元组转换为数组,数据类型由元素自动推断。
a = np.array([2, 3, 4])
print(a) # [2 3 4]
print(a.dtype) # int64
b = np.array([1.2, 3.5, 5.1])
print(b.dtype) # float64常见错误:np.array 接受单个序列参数,而不是多个参数。例如:
# 错误
np.array(1, 2, 3, 4) # TypeError: array() takes from 1 to 2 positional arguments but 4 were given
# 正确
np.array([1, 2, 3, 4]) # [1 2 3 4]嵌套序列会生成多维数组:
b = np.array([(1.5, 2, 3), (4, 5, 6)])
print(b)
# [[1.5 2. 3. ]
# [4. 5. 6. ]]可以显式指定数据类型:
c = np.array([[1, 2], [3, 4]], dtype=complex)
print(c)
# [[1.+0.j 2.+0.j]
# [3.+0.j 4.+0.j]]2. 使用占位符创建
NumPy 提供了创建初始内容的函数,适合快速生成大数组:
- np.zeros():创建全 0 数组。
- np.ones():创建全 1 数组。
- np.empty():创建内容随机的数组(取决于内存状态)。
print(np.zeros((3, 4)))
# [[0. 0. 0. 0.]
# [0. 0. 0. 0.]
# [0. 0. 0. 0.]]
print(np.ones((2, 3, 4), dtype=np.int16))
# [[[1 1 1 1]
# [1 1 1 1]
# [1 1 1 1]]
# [[1 1 1 1]
# [1 1 1 1]
# [1 1 1 1]]]
print(np.empty((2, 3))) # 内容随机
# [[3.73603959e-262 6.02658058e-154 6.55490914e-260]
# [5.30498948e-313 3.14673309e-307 1.00000000e+000]]3. 创建序列
- np.arange():类似 Python 的 range,但返回数组。
- np.linspace():生成指定数量的等间隔数字,适合浮点数。
print(np.arange(10, 30, 5)) # [10 15 20 25]
print(np.arange(0, 2, 0.3)) # [0. 0.3 0.6 0.9 1.2 1.5 1.8]
from numpy import pi
print(np.linspace(0, 2, 9)) # [0. 0.25 0.5 0.75 1. 1.25 1.5 1.75 2. ]
x = np.linspace(0, 2 * pi, 100)
f = np.sin(x) # 对 100 个点计算正弦值提示:arange 用于整数序列时简单高效;linspace 更适合浮点数,因为它能精确控制元素数量。
打印数组
NumPy 打印数组时,遵循以下规则:
- 最后一个轴:从左到右打印。
- 倒数第二个轴:从上到下打印。
- 其余轴:从上到下打印,每组切片之间有空行。
示例
# 一维数组
a = np.arange(6)
print(a) # [0 1 2 3 4 5]
# 二维数组
b = np.arange(12).reshape(4, 3)
print(b)
# [[ 0 1 2]
# [ 3 4 5]
# [ 6 7 8]
# [ 9 10 11]]
# 三维数组
c = np.arange(24).reshape(2, 3, 4)
print(c)
# [[[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]]
#
# [[12 13 14 15]
# [16 17 18 19]
# [20 21 22 23]]]对于大数组,NumPy 会省略中间部分,仅显示角落:
print(np.arange(10000).reshape(100, 100))
# [[ 0 1 2 ... 97 98 99]
# [ 100 101 102 ... 197 198 199]
# ...
# [9900 9901 9902 ... 9997 9998 9999]]禁用省略显示:
import sys
np.set_printoptions(threshold=sys.maxsize)基本运算
NumPy 的数组运算按 元素逐个进行,结果生成新数组。
逐元素运算
a = np.array([20, 30, 40, 50])
b = np.arange(4) # [0 1 2 3]
c = a - b
print(c) # [20 29 38 47]
print(b**2) # [0 1 4 9]
print(10 * np.sin(a)) # [ 9.12945251 -9.88031624 7.4511316 -2.62374854]
print(a < 35) # [ True True False False]矩阵运算
NumPy 的 * 是逐元素乘法,而矩阵乘法使用 @ 或 dot():
A = np.array([[1, 1], [0, 1]])
B = np.array([[2, 0], [3, 4]])
print(A * B) # 逐元素乘法
# [[2 0]
# [0 4]]
print(A @ B) # 矩阵乘法
# [[5 4]
# [3 4]]
print(A.dot(B)) # 等同于 @ 运算
# [[5 4]
# [3 4]]原地操作
某些操作(如 +=、*=)会直接修改原数组:
rg = np.random.default_rng(1)
a = np.ones((2, 3), dtype=int)
a *= 3
print(a) # [[3 3 3]
# [3 3 3]]
b = rg.random((2, 3))
b += a
print(b) # [[3.51182162 3.9504637 3.14415961]
# [3.94864945 3.31183145 3.42332645]]注意:类型不匹配时可能报错。例如,a += b 会因为 b 是浮点型而失败。
类型转换
不同类型数组运算时,结果类型会 向上转型 到更通用的类型:
a = np.ones(3, dtype=np.int32)
b = np.linspace(0, np.pi, 3)
print(b.dtype.name) # float64
c = a + b
print(c) # [1. 2.57079633 4.14159265]
print(c.dtype.name) # float64聚合操作
ndarray 提供方法计算统计值:
a = rg.random((2, 3))
print(a.sum()) # 3.1057109529998157
print(a.min()) # 0.027559113243068367
print(a.max()) # 0.8277025938204418按轴操作:
b = np.arange(12).reshape(3, 4)
print(b)
# [[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]]
print(b.sum(axis=0)) # 每列求和
# [12 15 18 21]
print(b.min(axis=1)) # 每行最小值
# [0 4 8]
print(b.cumsum(axis=1)) # 每行累加
# [[ 0 1 3 6]
# [ 4 9 15 22]
# [ 8 17 27 38]]通用函数(ufunc)
NumPy 的通用函数(ufunc)对数组进行逐元素运算,返回新数组。例如:
B = np.arange(3) # [0 1 2]
print(np.exp(B)) # [1. 2.71828183 7.3890561 ]
print(np.sqrt(B)) # [0. 1. 1.41421356]
C = np.array([2., -1., 4.])
print(np.add(B, C)) # [2. 0. 6.]常用 ufunc 包括:sin、cos、exp、sqrt、add 等。
索引、切片与迭代
一维数组
一维数组的索引和切片类似 Python 列表:
a = np.arange(10)**3
print(a) # [ 0 1 8 27 64 125 216 343 512 729]
print(a[2]) # 8
print(a[2:5]) # [ 8 27 64]
a[:6:2] = 1000 # 每隔两个元素赋值为 1000
print(a) # [1000 1 1000 27 1000 125 216 343 512 729]
print(a[::-1]) # 反转 [ 729 512 343 216 125 1000 27 1000 1 1000]迭代:
for i in a:
print(i**(1/3.))多维数组
多维数组的索引用逗号分隔:
def f(x, y):
return 10 * x + y
b = np.fromfunction(f, (5, 4), dtype=int)
print(b)
# [[ 0 1 2 3]
# [10 11 12 13]
# [20 21 22 23]
# [30 31 32 33]
# [40 41 42 43]]
print(b[2, 3]) # 23
print(b[0:5, 1]) # 第二列 [ 1 11 21 31 41]
print(b[:, 1]) # 同上
print(b[1:3, :]) # 第二、三行
# [[10 11 12 13]
# [20 21 22 23]]当索引不足时,缺失部分视为完整切片:
print(b[-1]) # 最后一行 [40 41 42 43]点号(…)
… 表示补全缺失的冒号。例如:
c = np.array([[[0, 1, 2], [10, 12, 13]],
[[100, 101, 102], [110, 112, 113]]])
print(c.shape) # (2, 2, 3)
print(c[1, ...]) # 等同于 c[1, :, :]
# [[100 101 102]
# [110 112 113]]
print(c[..., 2]) # 等同于 c[:, :, 2]
# [[ 2 13]
# [102 113]]迭代
多维数组默认沿第一个轴迭代:
for row in b:
print(row)逐元素迭代使用 flat:
for element in b.flat:
print(element)形状操作
查看形状
数组的形状由 shape 属性表示:
a = np.floor(10 * rg.random((3, 4)))
print(a)
# [[3. 7. 3. 4.]
# [1. 4. 2. 2.]
# [7. 2. 4. 9.]]
print(a.shape) # (3, 4)修改形状
以下方法可更改形状:
- ravel():展平为 1D 数组。
- reshape():更改形状,返回新数组。
- T:转置数组。
print(a.ravel()) # [3. 7. 3. 4. 1. 4. 2. 2. 7. 2. 4. 9.]
print(a.reshape(6, 2))
# [[3. 7.]
# [3. 4.]
# [1. 4.]
# [2. 2.]
# [7. 2.]
# [4. 9.]]
print(a.T)
# [[3. 1. 7.]
# [7. 4. 2.]
# [3. 2. 4.]
# [4. 2. 9.]]注意:reshape 返回新数组,resize 修改原数组:
a.resize((2, 6))
print(a)
# [[3. 7. 3. 4. 1. 4.]
# [2. 2. 7. 2. 4. 9.]]自动推断维度:
print(a.reshape(3, -1)) # -1 表示自动计算
# [[3. 7. 3. 4.]
# [1. 4. 2. 2.]
# [7. 2. 4. 9.]]数组堆叠与拆分
堆叠
vstack 和 hstack 用于沿不同轴堆叠数组:
a = np.floor(10 * rg.random((2, 2)))
b = np.floor(10 * rg.random((2, 2)))
print(np.vstack((a, b))) # 垂直堆叠
# [[9. 7.]
# [5. 2.]
# [1. 9.]
# [5. 1.]]
print(np.hstack((a, b))) # 水平堆叠
# [[9. 7. 1. 9.]
# [5. 2. 5. 1.]]column_stack 将 1D 数组按列堆叠为 2D:
a = np.array([4., 2.])
b = np.array([3., 8.])
print(np.column_stack((a, b)))
# [[4. 3.]
# [2. 8.]]拆分
hsplit 和 vsplit 用于拆分数组:
a = np.floor(10 * rg.random((2, 12)))
print(np.hsplit(a, 3)) # 分为 3 份
print(np.hsplit(a, (3, 4))) # 在第 3、4 列后拆分副本与视图
NumPy 操作数组时,可能涉及以下情况:
1. 无副本
简单赋值不复制数据:
a = np.array([[0, 1, 2, 3], [4, 5, 6, 7], [8, 9, 10, 11]])
b = a
print(b is a) # True2. 视图(浅副本)
视图共享数据,但可能是不同形状:
c = a.view()
print(c is a) # False
print(c.base is a) # True
c = c.reshape((2, 6))
c[0, 4] = 1234
print(a) # a 的数据被修改
# [[ 0 1 2 3]
# [1234 5 6 7]
# [ 8 9 10 11]]切片返回视图:
s = a[:, 1:3]
s[:] = 10
print(a)
# [[ 0 10 10 3]
# [1234 10 10 7]
# [ 8 10 10 11]]3. 深副本
copy() 创建完全独立的新数组:
d = a.copy()
print(d is a) # False
d[0, 0] = 9999
print(a) # a 不变高级索引
整数数组索引
使用整数数组选择元素:
a = np.arange(12)**2
i = np.array([1, 1, 3, 8, 5])
print(a[i]) # [ 1 1 9 64 25]
j = np.array([[3, 4], [9, 7]])
print(a[j]) # [[ 9 16]
# [81 49]]示例:调色板映射
palette = np.array([[0, 0, 0], [255, 0, 0], [0, 255, 0], [0, 0, 255], [255, 255, 255]])
image = np.array([[0, 1, 2, 0], [0, 3, 4, 0]])
print(palette[image])布尔索引
使用布尔数组选择元素:
a = np.arange(12).reshape(3, 4)
b = a > 4
print(b)
# [[False False False False]
# [False True True True]
# [ True True True True]]
print(a[b]) # [ 5 6 7 8 9 10 11]
a[b] = 0
print(a)
# [[0 1 2 3]
# [4 0 0 0]
# [0 0 0 0]]示例:曼德布洛特集
import matplotlib.pyplot as plt
def mandelbrot(h, w, maxit=20, r=2):
x = np.linspace(-2.5, 1.5, 4*h+1)
y = np.linspace(-1.5, 1.5, 3*w+1)
A, B = np.meshgrid(x, y)
C = A + B*1j
z = np.zeros_like(C)
divtime = maxit + np.zeros(z.shape, dtype=int)
for i in range(maxit):
z = z**2 + C
diverge = abs(z) > r
div_now = diverge & (divtime == maxit)
divtime[div_now] = i
z[diverge] = r
return divtime
plt.clf()
plt.imshow(mandelbrot(400, 400))
plt.show()技巧与提示
自动形状判断
使用 -1 自动推断维度:
a = np.arange(30)
b = a.reshape((2, -1, 3))
print(b.shape) # (2, 5, 3)向量堆叠
将向量堆叠为二维数组:
x = np.arange(0, 10, 2)
y = np.arange(5)
m = np.vstack([x, y])
print(m)
# [[0 2 4 6 8]
# [0 1 2 3 4]]直方图
生成并绘制直方图:
rg = np.random.default_rng(1)
mu, sigma = 2, 0.5
v = rg.normal(mu, sigma, 10000)
plt.hist(v, bins=50, density=True)
plt.show()
(n, bins) = np.histogram(v, bins=50, density=True)
plt.plot(.5 * (bins[1:] + bins[:-1]), n)
plt.show()错误检查与改进
- 原文错误:
- 部分代码中的注释(如 ../_images/quickstart-1.png)是文档生成器的占位符,已移除。
- np.random.default_rng 的用法在较旧版本 NumPy 中可能不兼容,建议使用 NumPy 1.17+。
- 部分中文翻译(如“通用”)不够直观,已改为“通用函数”。
- 面向新手的改进:
- 添加了安装说明和环境建议。
- 用 - 每段代码后增加了详细解释,帮助新手理解。
- 使用更通俗的语言,避免术语堆砌。
- 添加了可视化示例(如曼德布洛特集),让内容更生动。
结语
通过本教程,你应该已经掌握了 NumPy 的核心功能,包括数组创建、操作、索引和高级功能。NumPy 是科学计算的基石,熟练掌握它将为你的数据分析、机器学习等任务打下坚实基础。继续实践,探索 NumPy 的更多功能吧!
如果你有任何疑问或想深入学习某个部分,请留言或查阅 NumPy 官方文档!