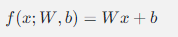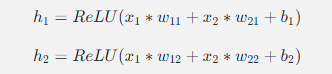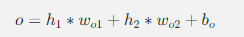【深度学习】神经网络拟合真实世界的过程!
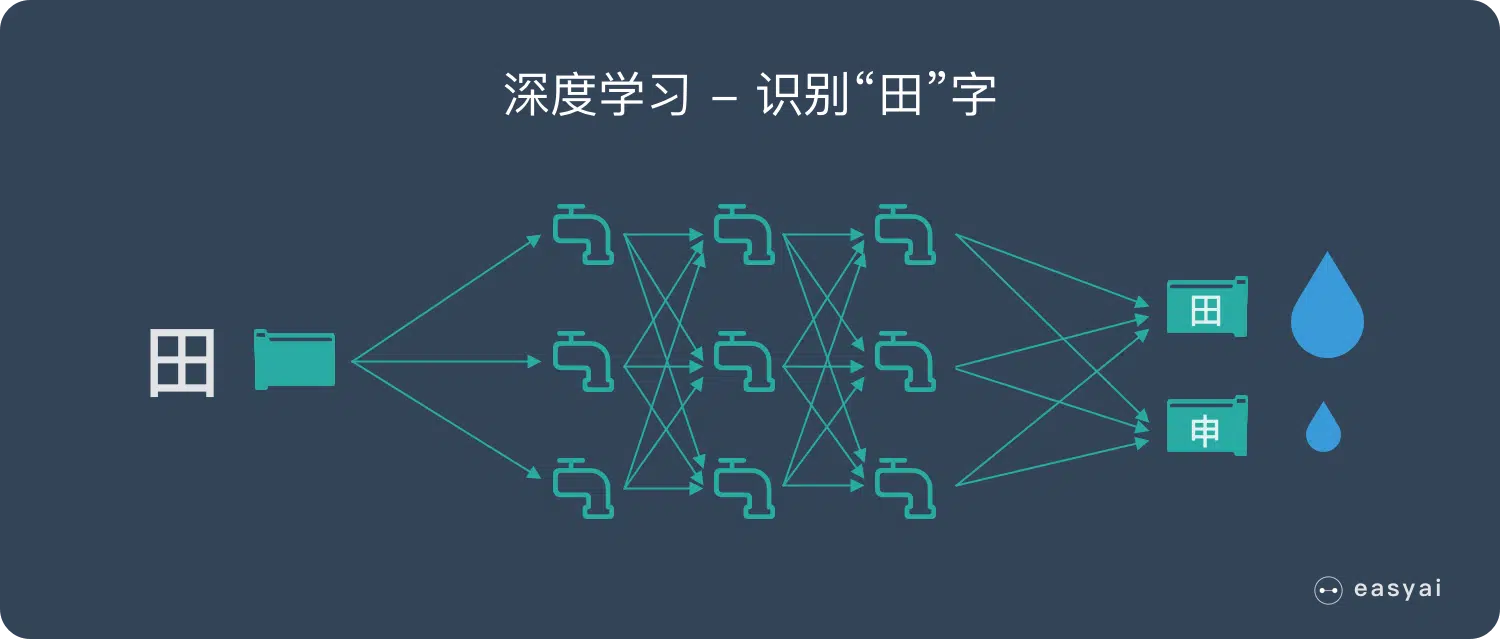
【深度学习】神经网络拟合真实世界的过程!
ytkz神经网络是一种强大的计算模型,它能够学习并拟合复杂的数据模式,从图像和文本到音频和更多。神经网络通过以下步骤来拟合现实世界的数据:
1.数字化。把真实物理世界的内容用数值来表示。
2.定义网络结构。通过模拟神经元的形式,构造神经网络。如何定义一个神经网络的好坏一般是由结果说明(在学术上缺少数学公式证明)。
3.前向传播。数据在多维空间中的函数映射,生产初步预测。
4.计算损失。计算初步预测与真实结果的差异。
5.反向传播和优化。目标是通过迭代更新网络参数(权重和偏置),以最小化预测输出和实际目标之间的差异。
6.迭代训练。以上过程在多个训练周期(称为”epochs”)中反复进行,每个周期都会遍历整个训练数据集。每个周期结束后,网络的权重和偏置会被更新,以减少预测和真实值之间的差异。
数字化
在神经网络的世界里,数据预处理就像是准备一场精彩的音乐会。我们需要将原始的、无序的音符(现实世界的数据)经过一系列的处理和调整,才能演奏出一曲动听的乐章(有效的模型)。
首先,我们需要进行”特征提取”,这就像是挑选音乐会的曲目。比如在文本分类任务中,我们把文字的词频和语义信息提取出来,就像是挑选出最能触动人心的旋律;在图像分类任务中,我们把像素强度和图像的高级特征提取出来,就像是将乐曲分成不同的乐章,以保证它们在音乐会中的和谐统一。
接着,我们需要进行”标准化”,这就像是调整音乐会的音量和节奏,使其达到最佳的效果。我们将特征缩放到同一范围,就像是调整音乐会的高低音,使其更适合神经网络的“听觉”。
然后,我们需要进行”数据分割”,这就像是将音乐会分配到不同的部分。训练集、验证集和测试集就像是音乐会的序曲、主体部分和尾声,每个部分都有其特定的角色。
最后,我们需要进行”编码”,这就像是给音乐会做最后的装饰。对于分类任务,我们将类别标签转化为神经网络可以理解的形式,就像是在音乐会上添加一些灯光和舞蹈,使其更具吸引力。
流程如下:
原始数据
|
v
特征提取(样本制作)
|
v
标准化
|
v
数据分割
|
v
编码
|
v
神经网络训练
定义网络结构
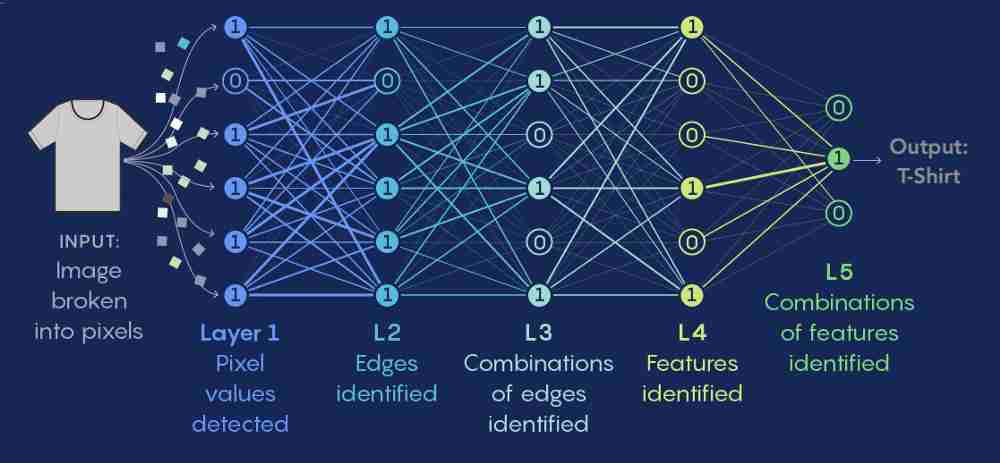
样本制作完成后,就到如何定义一个神经网络的结构,也被称为网络的架构或拓扑,是由多层的神经元(也称为节点)组成的。每个神经元都会对其输入数据进行一些计算,并产生一个输出。这些神经元按照特定的方式连接在一起,形成了神经网络的结构。以下是定义神经网络结构的关键组成部分:
1. 输入层
输入层是神经网络的第一层,它接收原始输入数据。输入层的神经元数量通常取决于特征的数量。例如,如果我们正在处理28x28像素的图像,那么输入层可能有784个神经元(因为28x28=784)。
2. 隐藏层
隐藏层位于输入层和输出层之间,可以有一个或多个。隐藏层的神经元数量和层数会影响网络的容量,即模型能够学习和表示的复杂度。每个隐藏层内的神经元都会接收来自前一层的输入,进行加权求和,并通过一个激活函数(如ReLU、sigmoid或tanh)进行非线性转换。
3. 输出层
输出层是神经网络的最后一层,它的神经元数量通常取决于任务的类型。例如,对于二分类问题,输出层可能只有一个神经元;对于多分类问题,输出层可能有与类别数量相等的神经元。
4. 连接和权重
神经元之间的连接由权重参数控制,这些权重在训练过程中被学习和调整。每个神经元还有一个偏置参数,它也在训练过程中被学习和调整。
神经网络的基本数学表示可以写为:
其中,x 是输入,W 是权重,b 是偏置,f是激活函数。
神经网络的结构和参数数量决定了模型的复杂度和容量。更深或更宽的网络可以表示更复杂的函数,但也更容易过拟合;相反,较小的网络可能无法充分学习数据中的模式,但是它们的计算效率更高,且更不容易过拟合。
向前传播
前向传播(Forward Propagation)是神经网络进行预测的过程。在这个过程中,输入数据从网络的输入层开始,经过一个或多个隐藏层,最后到达输出层。在每一层,数据都会与该层的权重相乘,然后加上偏置,最后通过一个激活函数。这个过程会在所有层中重复,直到达到输出层。
以下是一个简单的前向传播的例子。假设我们有一个只有一个隐藏层的神经网络,输入层有两个神经元,隐藏层有两个神经元,输出层有一个神经元。输入数据为(x1,x2),隐藏层的权重和偏置分别为w11,w12,w21,w22,b1,b2,输出层的权重和偏置为wo1,wo2,bo,激活函数为ReLU函数。
前向传播的过程如下:
- 计算隐藏层的值:
2.计算输出层的值:
计算损失
设想你正在玩一个箭靶游戏。你的目标是尽可能地接近靶心。每次你射出一支箭,你都会根据箭头离靶心的距离得到一个分数。箭头越接近靶心,你的分数就越高。这个分数就像是神经网络的负损失值,箭头离靶心的距离就像是损失值。
在神经网络中,我们的目标是让预测值尽可能地接近真实值。每次前向传播后,我们都会计算预测值与真实值之间的差距,这个差距就是损失值。我们的目标是通过调整网络的权重和偏置来最小化损失值。
损失函数的选择取决于我们的任务。例如,对于二分类问题,我们通常使用二元交叉熵损失函数;对于多分类问题,我们通常使用多元交叉熵损失函数;对于回归问题,我们通常使用均方误差损失函数。
以下是损失计算的流程示意图:
前向传播
|
v
计算预测值
|
v
计算损失值
反向传播和优化
假设你正在玩一个盲人摸象的游戏。你被蒙上眼睛,然后被放在一个房间里,房间里有一个大象。你的任务是通过摸索来了解大象的形状。这个游戏的规则是,你只能一次摸一个部分,然后根据你摸到的信息,你需要调整你对大象形状的猜测。
在这个游戏中,大象代表了数据,你的猜测代表了神经网络的预测,你的手代表了损失函数,你根据摸到的信息调整猜测的过程代表了反向传播和优化。
当你首次触摸大象时(前向传播),你可能会触摸到大象的腿,然后你可能会猜测大象的形状是像柱子一样的。然后,你会把你的手移动到其他部分(计算损失),比如大象的耳朵,然后你会发现你的猜测是错误的。然后,你需要根据你摸到的新信息(反向传播)来调整你的猜测,比如你可能会猜测大象的形状是像一个有大耳朵的柱子。这个调整猜测的过程就是优化。
在神经网络中,我们首先进行前向传播,然后计算损失,然后通过反向传播来计算损失函数的梯度,然后通过优化算法(如梯度下降)来更新网络的权重和偏置,以减少未来的损失。
以下是反向传播和优化的流程示意图:
前向传播 ——> 计算损失
| |
v v
反向传播 <—— 更新权重和偏置(优化)
在这个过程中,我们首先进行前向传播,然后计算损失,然后通过反向传播来计算损失函数的梯度,然后通过优化算法(如梯度下降)来更新网络的权重和偏置。希望这个比喻和示意图可以帮助你更好地理解反向传播和优化的过程。
迭代训练
以下是迭代训练的流程示意图:
初始化模型
|
v
预测 ——> 计算损失
| |
v v
反向传播 <—— 更新权重和偏置(优化)
|
v
重复以上步骤
在迭代训练过程中,我们首先需要初始化模型的参数。这可以是随机的,也可以是基于某种策略的,这取决于特定的模型和任务。
初始化完成后,我们使用这些初始参数对输入数据进行预测。这个预测过程也被称为前向传播,因为信息从输入层流向输出层。
一旦我们得到预测结果,我们就需要计算这些预测与真实值之间的差距,这个差距就是我们的损失。损失函数的形式取决于我们的任务,例如,对于回归任务,我们可能使用均方误差作为损失函数。
接下来,我们需要找出如何调整模型参数以减少这种损失。这是通过计算损失函数相对于模型参数的梯度来完成的,这个过程就是所谓的反向传播。
一旦我们计算出了梯度,我们就可以使用这些梯度来更新我们的模型参数。这个过程被称为优化。最常用的优化算法是梯度下降,它会根据梯度的方向和大小来调整模型参数。
这个过程(预测,计算损失,反向传播,优化)会在每个训练迭代中重复。每一次迭代,模型的参数都会被更新,以减少损失并改进预测。这个过程会一直进行,直到模型的性能达到满意的水平,或者达到预设的迭代次数。