【代码】计算地理多边形在地球表面的面积的Python代码解析
【代码】计算地理多边形在地球表面的面积的Python代码解析
ytkz我们现在要探索的是一个名为”area”的Python包。这个包的主要功能是计算地理多边形在地球表面的面积。为了深入理解其工作原理,我们将直接研究这个包的源代码,特别关注它是如何根据给定的经纬度来计算地理多边形的面积。这将是一个深入学习Python编程以及地理信息处理的绝佳机会。
以下是添加中文注释后的代码:
from __future__ import division # 使得除法的结果为浮点数,即使两个操作数都是整数
import json # 用于处理JSON格式的数据
from math import pi, sin # 导入数学库中的圆周率和正弦函数
__version__ = '1.1.1' # 版本信息
WGS84_RADIUS = 6378137 # 定义WGS84椭球体赤道半径,单位是米
def rad(value): # 定义一个函数,将角度转换为弧度
return value * pi / 180
def ring__area(coordinates): # 计算一个环的面积
assert isinstance(coordinates, (list, tuple)) # 断言坐标必须是列表或元组类型
_area = 0 # 初始化面积为0
coordinates_length = len(coordinates) # 获取坐标的数量
if coordinates_length > 2: # 如果坐标数量大于2,即多边形至少有3个顶点
for i in range(0, coordinates_length): # 遍历所有的坐标
if i == (coordinates_length - 2): # 如果当前是倒数第二个坐标
lower_index = coordinates_length - 2
middle_index = coordinates_length - 1
upper_index = 0
elif i == (coordinates_length - 1): # 如果当前是最后一个坐标
lower_index = coordinates_length - 1
middle_index = 0
upper_index = 1
else: # 其他情况
lower_index = i
middle_index = i + 1
upper_index = i + 2
p1 = coordinates[lower_index] # 获取三个坐标点
p2 = coordinates[middle_index]
p3 = coordinates[upper_index]
_area += (rad(p3[0]) - rad(p1[0])) * sin(rad(p2[1])) # 计算面积
_area = _area * WGS84_RADIUS * WGS84_RADIUS / 2 # 将面积转换为实际面积
return _area # 返回面积
def polygon__area(coordinates): # 计算一个多边形的面积
assert isinstance(coordinates, (list, tuple)) # 断言坐标必须是列表或元组类型
_area = 0 # 初始化面积为0
if len(coordinates) > 0: # 如果坐标数量大于0
_area += abs(ring__area(coordinates[0])) # 计算并添加第一个环(通常是外环)的面积
for i in range(1, len(coordinates)): # 遍历剩余的环(通常是内环,即“洞”)
_area -= abs(ring__area(coordinates[i])) # 计算并减去每个“洞”的面积
return _area # 返回面积
def area(geometry): # 计算一个几何形状的面积
if isinstance(geometry, str): # 如果输入是字符串
geometry = json.loads(geometry) # 将字符串转换为字典
assert isinstance(geometry, dict) # 断言几何形状必须是字典类型
_area = 0 # 初始化面积为0
if geometry['type'] == 'Polygon': # 如果几何形状是多边形
return polygon__area(geometry['coordinates']) # 计算并返回多边形的面积
elif geometry['type'] == 'MultiPolygon': # 如果几何形状是多个多边形
for i in range(0, len(geometry['coordinates'])): # 遍历每个多边形
_area += polygon__area(geometry['coordinates'][i]) # 计算并添加每个多边形的面积
# 如果几何形状是几何集合
elif geometry['type'] == 'GeometryCollection':
for i in range(0, len(geometry['geometries'])): # 遍历每个子形状
_area += area(geometry['geometries'][i]) # 递归地计算并添加每个子形状的面积
return _area # 返回面积代码解析
这段Python代码是用来计算地理多边形(如地图上的国家、省份、城市等区域)在地球表面的面积的。它支持多种地理形状,包括单个多边形(Polygon)、多个多边形(MultiPolygon)和几何集合(GeometryCollection)。
这段代码的主要工作原理是将地球视为一个球体,并使用球面多边形面积公式来计算面积。这种方法的精度对于大多数应用来说是足够的,但对于需要极高精度的应用,可能需要使用更复杂的模型,如椭球模型。
具体来说,这段代码包含以下几个函数:
rad(value): 将角度转换为弧度。ring__area(coordinates): 计算一个多边形(由一系列坐标点定义)在地球表面的面积。这个函数使用了Chamberlain和Duquette在2007年的论文中描述的方法。这个方法的基本思想是使用球面三角形的面积公式来近似计算多边形的面积。polygon__area(coordinates): 计算一个多边形或者一个带有孔的多边形(由一系列环定义)在地球表面的面积。对于带有孔的多边形,这个函数会先计算外环的面积,然后减去每个孔的面积。area(geometry): 根据输入的地理形状类型,调用适当的函数来计算面积。这个函数支持多边形(Polygon)、多个多边形(MultiPolygon)和几何集合(GeometryCollection)。对于几何集合,这个函数会递归地计算每个子形状的面积,并将它们相加。
如何使用
安装area
pip install area接受一个字典作为输入,该字典表示一个几何形状,其格式符合GeoJSON规范。
以下是一个简单的使用示例:
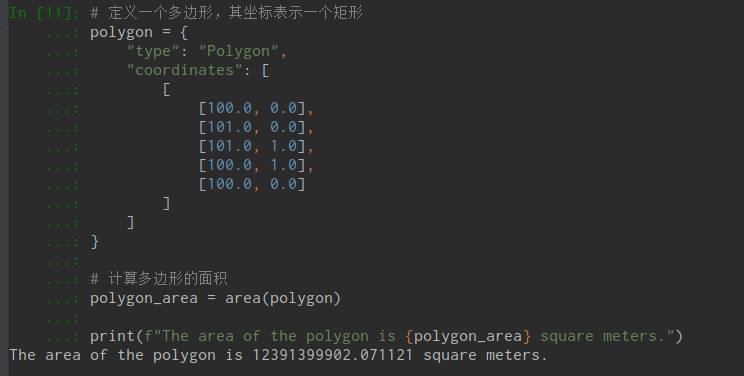
# 定义一个多边形,其坐标表示一个矩形
polygon = {
"type": "Polygon",
"coordinates": [
[
[100.0, 0.0],
[101.0, 0.0],
[101.0, 1.0],
[100.0, 1.0],
[100.0, 0.0]
]
]
}
# 计算多边形的面积
polygon_area = area(polygon)
print(f"The area of the polygon is {polygon_area} square meters.")另外,这个代码还可以处理”MultiPolygon”和”GeometryCollection”类型的几何形状。”MultiPolygon”类型的几何形状包含多个多边形,每个多边形的坐标是一个二维列表,表示多边形的所有顶点,每个顶点是一个长度为2的列表,表示顶点的经度和纬度。”GeometryCollection”类型的几何形状包含多个子形状,每个子形状可以是任何类型的几何形状,包括”Polygon”、”MultiPolygon”和”GeometryCollection”。