利用Python处理合成孔径雷达(SAR)数据的成像过程
利用Python处理合成孔径雷达(SAR)数据的成像过程
ytkz本文介绍了利用Python处理合成孔径雷达(SAR)数据的完整流程,包括数据加载、基本定义、聚焦、多视处理和结果显示等步骤。
首先,通过加载包含SAR原始数据的.mat文件,获取数据矩阵并设置相关的传感器参数。
接着,定义了两个主要脉冲,即距离向脉冲和方位向脉冲,并对其进行傅里叶变换和共轭运算,得到用于后续相关处理的脉冲模板。
在数据聚焦步骤中,通过距离向和方位向的压缩操作,将原始数据转化为聚焦后的图像。
为了进一步降低噪声、提高图像质量,代码还实现了多视处理,通过空间平均来平滑数据。
最后,通过对处理后的数据进行归一化和对比度调整,将结果显示为灰度图像。
整个过程展示了SAR数据处理的基本步骤和原理,为从事SAR成像和数据处理的研究人员和工程师提供了一个完整的技术实现参考。
现在直接把完整的代码放出来,并附上一份
完整代码
#!c:/Python/python.exe
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import scipy.io as spio
import math as math
from matplotlib import cm
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['STZhongsong'] # 指定默认字体:解决plot不能显示中文问题
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# --------------------------------------------------
def display_raw_data(Raw_data):
# 显示原始数据
Raw_data_abs = abs(Raw_data)
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.imshow(Raw_data_abs, aspect='equal', cmap=cm.gray)
ax.set_title('原始数据(未聚焦)')
ax.set_xlabel('距离像素')
ax.set_ylabel('方位像素')
ax.set_xticks([])
ax.set_yticks([])
def basic_definitions(fs, K_r, tau_p, V, Lambda, R_0, ta, prf):
range_chirp = np.zeros((1, size_range), 'complex') # 创建一个空向量用于存储距离向的脉冲
tau = np.arange(-tau_p / 2, tau_p / 2, 1 / fs) # 距离向的时间轴
omega = np.arange(-fs / 2, fs / 2, 1 / tau_p) # 距离向的频率轴
# 定义距离向的脉冲
phase = 1j * math.pi * K_r * tau ** 2
ra_chirp_temp = np.exp(phase)
# 获取脉冲的大小
size_chirp_r = len(tau)
# 显示距离向的脉冲(时间域和频率域)
# 时间域
fig = plt.figure()
ax2 = fig.add_subplot(2, 1, 1)
ax2.plot(tau, ra_chirp_temp.real, 'b')
ax2.plot(tau, ra_chirp_temp.imag, 'r')
ax2.set_title('距离向脉冲')
ax2.set_xlabel('时间轴 [秒]')
ax2.set_ylabel('幅度')
# 频率域
Spectrum_temp = abs(np.fft.fftshift(np.fft.fft(ra_chirp_temp))) # 傅里叶变换
ax3 = fig.add_subplot(2, 1, 2)
ax3.plot(omega, Spectrum_temp)
ax3.set_title('距离向脉冲的频谱')
ax3.set_xlabel('频率 [Hz]')
ax3.set_ylabel('绝对值')
# 将脉冲定位在距离向向量的中心
index_start = np.ceil((size_range - size_chirp_r) / 2) - 1
index_end = size_chirp_r + np.ceil((size_range - size_chirp_r) / 2) - 2
range_chirp[0, int(index_start):int(index_end) + 1] = ra_chirp_temp
RANGE_CHIRP = np.fft.fft(range_chirp) # 傅里叶变换
# 定义用于相关处理的脉冲
CON_RANGE_CHIRP = np.conjugate(RANGE_CHIRP)
azimuth_chirp = np.zeros((1, size_azimuth), 'complex') # 创建一个空向量用于存储方位向的脉冲
t = np.arange(-ta / 2, ta / 2, 1 / prf) # 方位向的时间轴
v = np.arange(-prf / 2, prf / 2, 1 / ta) # 方位向的频率轴
# 方位向脉冲的调频率
K_a = (-2 * V ** 2) / (Lambda * R_0)
# 定义方位向的脉冲
phase2 = 1j * math.pi * K_a * t ** 2
az_chirp_temp = np.exp(phase2)
# 获取脉冲的大小
size_chirp_a = len(t)
# 显示方位向的脉冲(时间域和频率域)
# 时间域
fig = plt.figure()
ax4 = fig.add_subplot(2, 1, 1)
ax4.plot(t, az_chirp_temp.real, 'b')
ax4.plot(t, az_chirp_temp.imag, 'r')
ax4.set_title('方位向脉冲')
ax4.set_xlabel('时间轴 [秒]')
ax4.set_ylabel('幅度')
# 频率域
Spectrum_temp2 = abs(np.fft.fftshift(np.fft.fft(az_chirp_temp))) # 傅里叶变换
ax5 = fig.add_subplot(2, 1, 2)
ax5.plot(v, Spectrum_temp2)
ax5.set_title('方位向脉冲的频谱')
ax5.set_xlabel('频率 [Hz]')
ax5.set_ylabel('绝对值')
# 将脉冲定位在方位向向量的中心
index_start2 = np.ceil((size_azimuth - size_chirp_a) / 2) - 1
index_end2 = size_chirp_a + np.ceil((size_azimuth - size_chirp_a) / 2) - 2
azimuth_chirp[0, int(index_start2):int(index_end2) + 1] = az_chirp_temp
AZIMUTH_CHIRP = np.fft.fft(azimuth_chirp) # 傅里叶变换
# 定义用于相关处理的脉冲
CON_AZIMUTH_CHIRP = np.conjugate(AZIMUTH_CHIRP)
return CON_RANGE_CHIRP, CON_AZIMUTH_CHIRP
def Focusing(CON_RANGE_CHIRP, CON_AZIMUTH_CHIRP, size_azimuth, size_range):
processed = np.zeros((size_azimuth, size_range), 'complex')
# 距离向压缩
for k1 in range(0, size_azimuth, 1):
vek = Raw_data[k1, :] # 选择距离向的行
VEK = np.fft.fft(vek) # 傅里叶变换
CORR = VEK * CON_RANGE_CHIRP # 乘以共轭复数
if_vek = np.fft.ifft(CORR) # 逆傅里叶变换
if_vek_sort = np.fft.ifftshift(if_vek) # 排序
processed[k1, :] = if_vek_sort # 存储行
# 方位向压缩
for k2 in range(0, size_range, 1):
vek2 = processed[:, k2] # 选择方位向的行
VEK2 = np.fft.fft(vek2)
CORR2 = VEK2 * CON_AZIMUTH_CHIRP
if_vek2 = np.fft.ifft(CORR2)
if_vek2_sort = np.fft.ifftshift(if_vek2)
processed[:, k2] = if_vek2_sort
return processed
def multilooking(processed, multilook):
if multilook == 1:
# 定义输出图像的大小
output_image = np.zeros((int(np.ceil(size_azimuth / ml_factor)), size_range), 'complex')
# 空间平均
index = 0
for i in range(0, size_azimuth - ml_factor, ml_factor):
vek = processed[i:i + (ml_factor - 1), ] # 选择方位向的行
m_vek = np.mean(vek, axis=0) # 计算方位向的平均值
output_image[index, :] = m_vek
index += 1
# 最终的SAR图像(多视处理)
processed = output_image
return processed
def displat_result(processed):
processed_abs = abs(processed) # 取绝对值
fig = plt.figure()
ax6 = fig.add_subplot(111)
processed_abs = (processed_abs - np.percentile(processed_abs, 2)) / (
np.percentile(processed_abs, 98) - np.percentile(processed_abs, 2)) * 255
processed_abs = np.uint8(processed_abs)
cax6 = ax6.imshow(processed_abs)
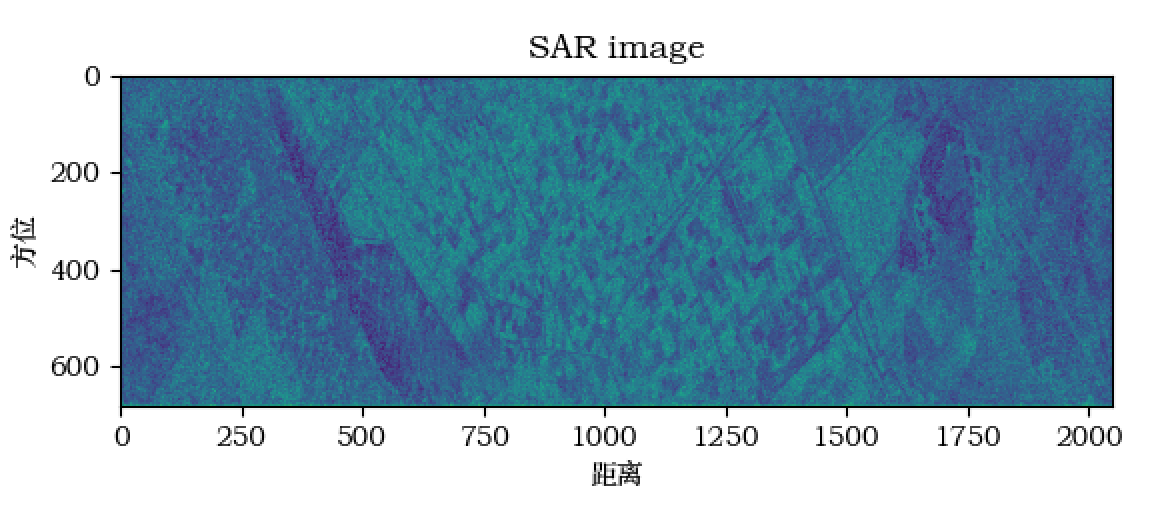
ax6.set_title('SAR image')
ax6.set_xlabel('距离')
ax6.set_ylabel('方位')
plt.show()
if __name__ == '__main__':
# A.) 加载原始数据
data = spio.loadmat(r'ERS.mat')
Raw_data = data['raw']
max_power = 10000
# 多视处理开关
multilook = 1 # 0: 关闭; 1: 开启
ml_factor = 3 # 多视处理因子(空间)
# 获取图像大小
size_azimuth = Raw_data.shape[0]
size_range = Raw_data.shape[1]
# B.) 传感器参数(ERS卫星)
fs = 18.962468 * 10 ** 6 # 距离采样频率 [Hz]
K_r = 4.18989015 * 10 ** 11 # 距离脉冲调频率 [1/s^2]
tau_p = 37.12 * 10 ** (-6) # 脉冲时长 [s]
V = 7098.0194 # 有效卫星速度 [m/s]
Lambda = 0.05656 # 载波波长 [m]
R_0 = 852358.15 # 天线脚点中心到目标距离 [m]
ta = 0.6 # 孔径时间 [s]
prf = 1679.902 # 脉冲重复频率 [Hz]
display_raw_data(Raw_data)
CON_RANGE_CHIRP, CON_AZIMUTH_CHIRP = basic_definitions(fs, K_r, tau_p, V, Lambda, R_0, ta, prf)
processed = Focusing(CON_RANGE_CHIRP, CON_AZIMUTH_CHIRP, size_azimuth, size_range)
processed = multilooking(processed, multilook)
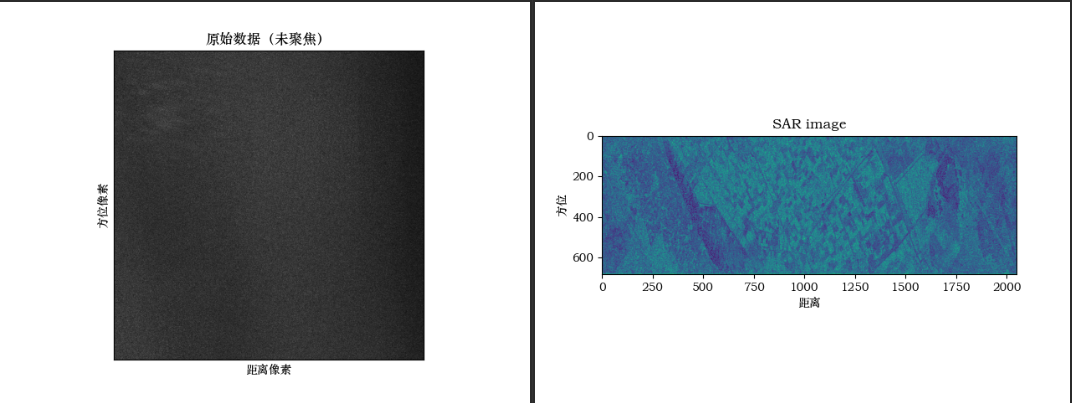
displat_result(processed)原始数据可视化与结果可视化对比
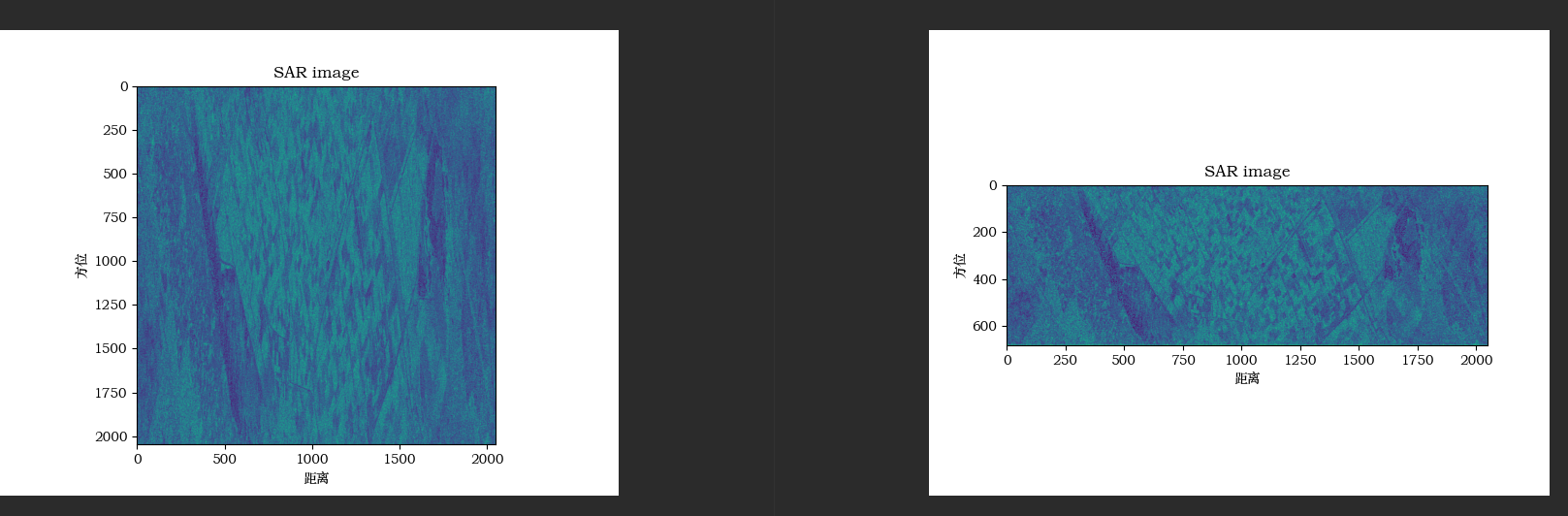
不进行多视处理与进行多视处理的对比:
结果如下图:
测试数据下载地址:
结论
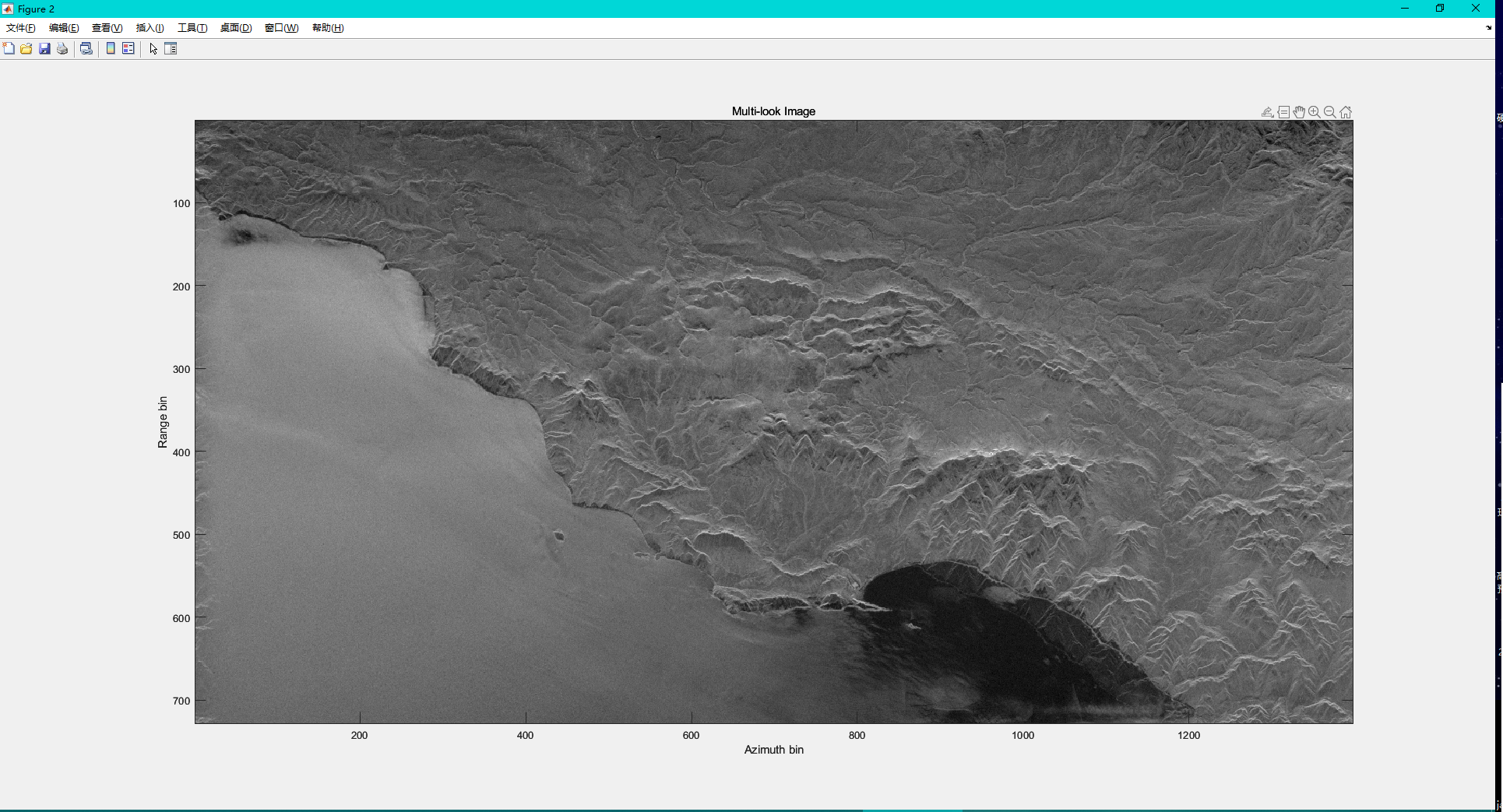
之前写过基于matlab的合成孔径雷达(SAR)的成像的内容,而现在这篇是关于利用Python处理合成孔径雷达(SAR)数据的完整流程,包括数据加载、基本定义、聚焦、多视处理和结果显示等内容。
学习SAR是出自于对SAR技术的看好,及拓展自身知识范围。但是隔行如隔山(光学遥感和雷达遥感其实不算是同行),SAR成像其实还好,难度大的是INSAR。说的就是你,解缠。解缠的公式是优美的,同时也是令人苦恼的。
人的精力是有限的,以后短时间内不会再写关于SAR的内容了,而是把精力更多地放在深度学习这个方面上。
收工。
(完)